What is Zipf’s mysterious law that finds mathematical patterns in random events?

There is a surprising pattern in the origin of the winners of the world’s most famous cycling race, andl Tour de France.

Runners from different countries around the world compete against each other for three weeks in a race that This Sunday the Slovenian Tadej Pogacar won.

Along with billions of others, I enjoy watching the spectacle of these almost superhuman athletes pushing themselves to the absolute limit on beautiful French soil.

While reading about the race, I came across a chart I hadn’t seen before: the number of Tour wins by nation. What caught my eye was the gentle arc-shaped descent of the curve from left to right.

In particular, I noticed that Belgium, the country ranked second in terms of victories with 18, had exactly half of the 36 victories achieved by French riders. The country with the next highest number of yellow jerseys, Spain, had exactly one-third (12) of France’s number of victories. Italy, the next nation on the list, had barely one-quarter (10) of the number of French victories.

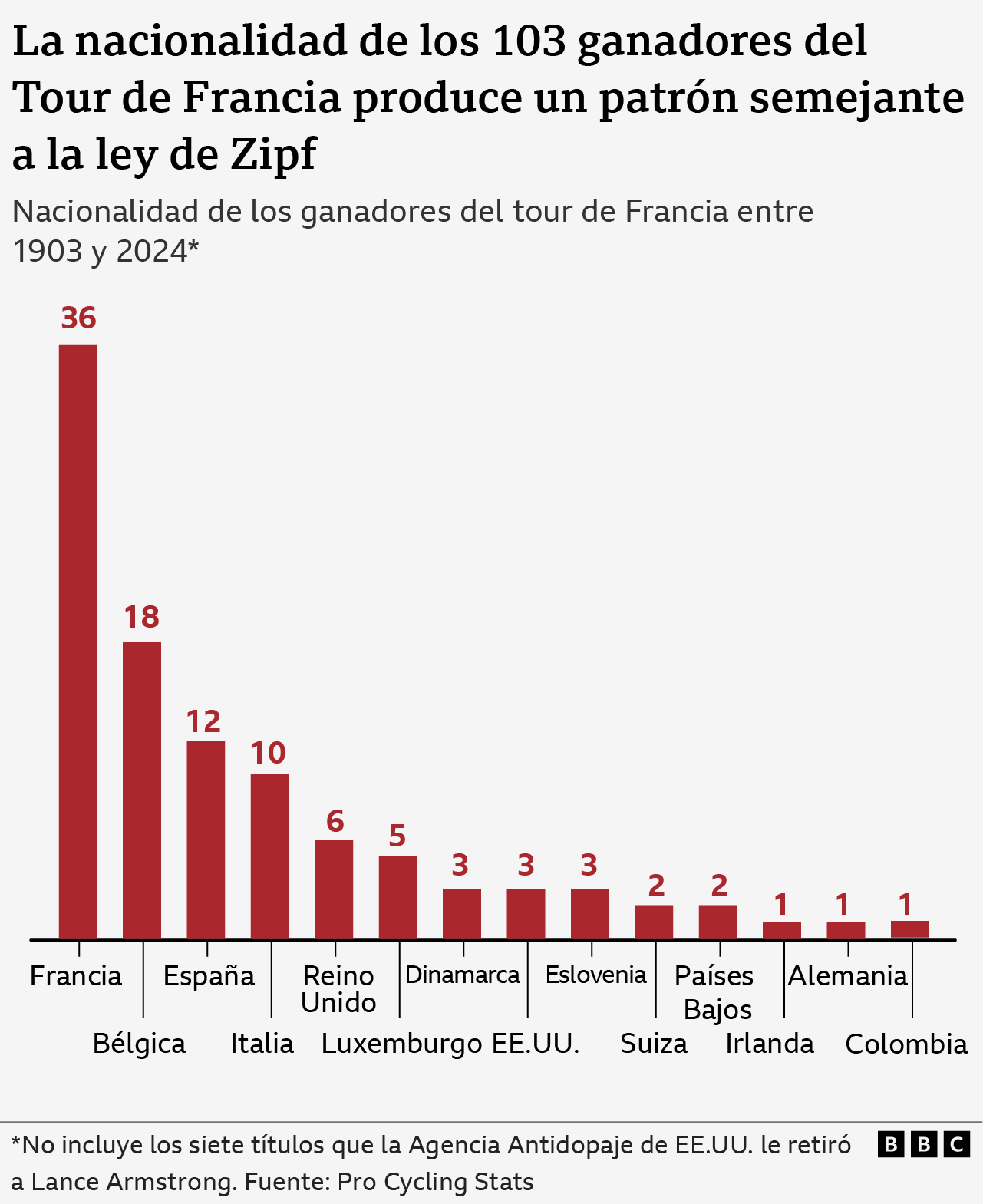
This reminded me a lot of a mysterious and ubiquitous distribution that many real-world data sets seem to fit. It’s called Zipf’s law and is best known for characterizing the frequency of appearance of words in a text.

In this context, Zipf’s law states that when words in a sufficiently long text are arranged in order of decreasing frequency, they exhibit a special pattern.

Specifically, the second most frequent word appears about half as often as the number one word. The third most frequent word appears about a third as often as the first, the fourth a quarter as often, and so on. Just like the winners of the Tour de France.

To test this, I looked at the word frequency of one of my own books, “The Maths of Life and Death.”, and I found a surprisingly good agreement with Zipf’s law.

The word I used most in the book was “the,” which occurred 6,691 times. In second place was “of,” which occurred 3,330 times, almost exactly half the number of times that “the” occurred. The word “to” was next, with 2,445 occurrences, just over a third as often as “the,” and so on.

By the way, the words “life” and “mathematics” appeared 64 times, while “death” appeared only 42 times, even though the title of the book was “The Mathematics of Life and Death.”

Even looking at the paragraphs above, we can see that there are some extremely common words, such as “la” and “el”mixed with more unusual words like “surprisingly” and “apparitions.”

In a long enough text, what Zipf’s law tells us is that there are many more rare words than common words.

In fact, Zipf’s law suggests that these factors balance each other out, so that if we draw a random word from a text, it is equally likely to be either one of the many rare words or one of the few common ones.

Zipf’s law for word frequency in a long text is universal. That is to say, it is not only valid for English, but apparently for many other languages, including Esperanto, which is an artificial language.

Curiously, this almost magical relationship is not limited to the words of a text or the Tour de France. It has been reported in extremely diverse scenarios, such as the number of articles written by scientists, the size of the population in settlements and even the diameter of craters on the Moon..

Zipf’s law is a special case of a more general rule: the power law.

In this context, such power laws suggest that one variable (e.g., the strength of the Earth’s gravitational pull) varies inversely proportionally in relation to some other variable (the distance from the center of the Earth) raised to some mathematical “power.” In the case of gravity, the shorter the distance from the center of the Earth, the stronger the pull, while the greater the distance, the weaker the pull.

Zipf’s power law for words in a long text is a special case where the “power” or “exponent” in the power law is one. This means that doubling one variable halves the other, tripling the first decreases the second by a third, and so on.

However, for a general power law, this is usually not the case. The inverse square law of gravitation, for example, follows a power law whose exponent (or power) is two. If you were to move twice as far away from the center of the Earth compared to where you are currently sitting, then the force you would experience at your new position would be four (two squared) times weaker than where you are now. If you move three times as far away, the force will be nine (three squared) times weaker, and so on.

Power laws have been found to describe a wide range of naturally generated data sets, from the variation in species diversity by habitat area to the frequency of the number of tornadoes per day in the United States and even the number of artists based on the average price of their work..

But there is more. Analyzing data on wars between 1809 and 1949, Lewis Richardson found that The frequency of fatal conflicts varied with respect to the number of people killed under the power law raised to ½Wars in which 1 million people died were 10 times less likely than those in which 10,000 people died and 100 times less likely than conflicts in which 100 people died.

Perhaps one of the most important power laws ever discovered was that published by Charles Richter and Beno Gutenberg in 1956, which describes how the frequency of earthquakes varies with their magnitude.

It is clear that power laws are important for describing a wide range of real-world phenomena, but Why do they seem to be so ubiquitous?

Mathematically it can be shown that power laws arise when systems exhibit either scale invariance or self-similarity.Systems that exhibit these related properties look the same (or more or less the same) when we zoom in or out on them.

Many real-world phenomena, from networks like the Internet to natural physical phenomena like snowflakes and biological structures like ferns, exhibit self-similar properties.

Power laws mathematically capture this self-similar property..

What may be the most compelling explanation for Zipf’s law holds that There are latent or unobserved variables that function to mix multiple components that, taken alone, would not obey this law, but when combined, they do..

In the context of word frequency, for example, components are the different parts of speech (e.g., adjectives, conjunctions, nouns, prepositions, verbs, etc.). For example, because they are general and used in sentences regardless of context, there are very few different conjunctions (e.g., “and,” “because”), each of which is relatively common. In contrast, although there are many more nouns (e.g., “speech,” “law,” etc.), each of them can only be used in specific contexts that are relatively uncommon.

Individually, these components do not obey Zipf’s law, but when these parts of speech are mixed with others to form language, they do.

The Tour de France is not the only sporting context in which Zipf’s law applies. It occurs in situations such as Olympic medals and prize money in billiards..

But it is not clear exactly why Zipf’s law applies to the Tour de France winners. Indeed, as expected, when the Zipf distribution is plotted on the actual data, the agreement is not perfect.

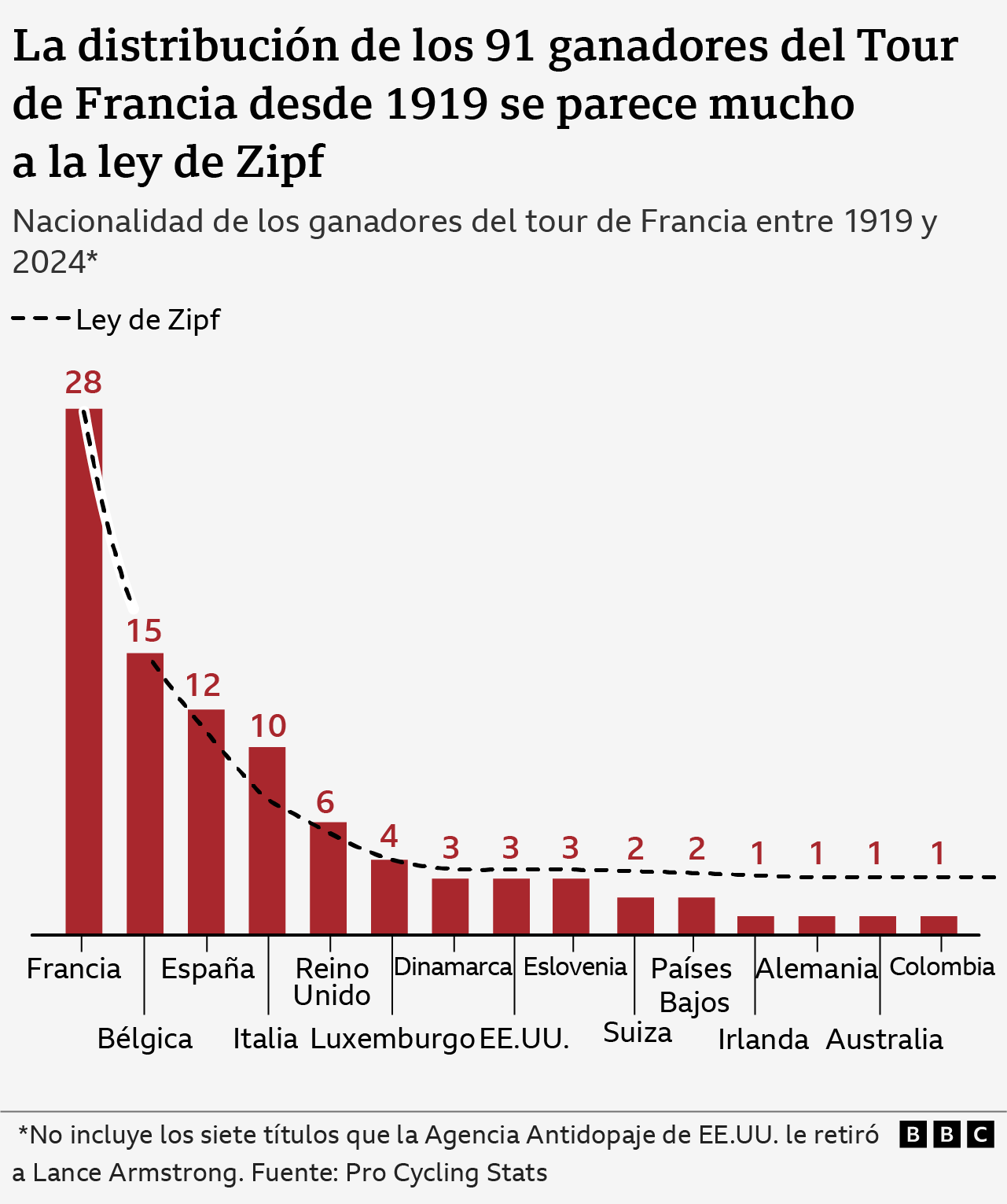
The European nations – France, Belgium, Spain and Italy – that have won the most Tour de France are over-represented. In one sense this is not surprising: the composition of the first Tours of France was dominated by the French and later by their neighbouring countries. In the first edition of the Tour in 1903, for example, 49 of the 60 cyclists entered were French..

In fact, if we eliminate all the winners before World War I, we can find that Zipf’s law fits better.

Since there has been no French winner of its most famous sporting event since 1985, some of the underrepresented nations have been given the chance to take their place in the distribution.

But what does this mean for next year’s race? Which country will win? Unfortunately, Zipf’s law only speaks in generalities and does not offer answers to such specific questions.

What is certain is that, whatever happens, it will take many years for the evidence of France’s early dominance of the Tour to fade from the data.

*Kit Yates is Director of the Centre for Biological Mathematics at the University of Bath and author of The Maths of Life and Death and How to Expect the Unexpected.

This is a Spanish adaptation of an essay published by BBC Future. If you want to check it out in its original English, you can find it here here.